Note
Go to the end to download the full example code.
Layer Normalization¶
In this tutorial, you will write a high-performance layer normalization kernel that runs faster than the PyTorch implementation.
In doing so, you will learn about:
Implementing backward pass in Triton.
Implementing parallel reduction in Triton.
Motivations¶
The LayerNorm operator was first introduced in [BA2016] as a way to improve the performance of sequential models (e.g., Transformers) or neural networks with small batch size. It takes a vector \(x\) as input and produces a vector \(y\) of the same shape as output. The normalization is performed by subtracting the mean and dividing by the standard deviation of \(x\). After the normalization, a learnable linear transformation with weights \(w\) and biases \(b\) is applied. The forward pass can be expressed as follows:
where \(\epsilon\) is a small constant added to the denominator for numerical stability. Let’s first take a look at the forward pass implementation.
import torch
import triton
import triton.language as tl
try:
# This is https://github.com/NVIDIA/apex, NOT the apex on PyPi, so it
# should not be added to extras_require in setup.py.
import apex
HAS_APEX = True
except ModuleNotFoundError:
HAS_APEX = False
@triton.jit
def _layer_norm_fwd_fused(
X, # pointer to the input
Y, # pointer to the output
W, # pointer to the weights
B, # pointer to the biases
Mean, # pointer to the mean
Rstd, # pointer to the 1/std
stride, # how much to increase the pointer when moving by 1 row
N, # number of columns in X
eps, # epsilon to avoid division by zero
BLOCK_SIZE: tl.constexpr,
):
# Map the program id to the row of X and Y it should compute.
row = tl.program_id(0)
Y += row * stride
X += row * stride
# Compute mean
mean = 0
_mean = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
for off in range(0, N, BLOCK_SIZE):
cols = off + tl.arange(0, BLOCK_SIZE)
a = tl.load(X + cols, mask=cols < N, other=0.).to(tl.float32)
_mean += a
mean = tl.sum(_mean, axis=0) / N
# Compute variance
_var = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
for off in range(0, N, BLOCK_SIZE):
cols = off + tl.arange(0, BLOCK_SIZE)
x = tl.load(X + cols, mask=cols < N, other=0.).to(tl.float32)
x = tl.where(cols < N, x - mean, 0.)
_var += x * x
var = tl.sum(_var, axis=0) / N
rstd = 1 / tl.sqrt(var + eps)
# Write mean / rstd
tl.store(Mean + row, mean)
tl.store(Rstd + row, rstd)
# Normalize and apply linear transformation
for off in range(0, N, BLOCK_SIZE):
cols = off + tl.arange(0, BLOCK_SIZE)
mask = cols < N
w = tl.load(W + cols, mask=mask)
b = tl.load(B + cols, mask=mask)
x = tl.load(X + cols, mask=mask, other=0.).to(tl.float32)
x_hat = (x - mean) * rstd
y = x_hat * w + b
# Write output
tl.store(Y + cols, y, mask=mask)
Backward pass¶
The backward pass for the layer normalization operator is a bit more involved than the forward pass. Let \(\hat{x}\) be the normalized inputs \(\frac{ x - \text{E}[x] }{ \sqrt{\text{Var}(x) + \epsilon} }\) before the linear transformation, the Vector-Jacobian Products (VJP) \(\nabla_{x}\) of \(x\) are given by:
where \(\odot\) denotes the element-wise multiplication, \(\cdot\) denotes the dot product, and \(\sigma\) is the standard deviation. \(c_1\) and \(c_2\) are intermediate constants that improve the readability of the following implementation.
For the weights \(w\) and biases \(b\), the VJPs \(\nabla_{w}\) and \(\nabla_{b}\) are more straightforward:
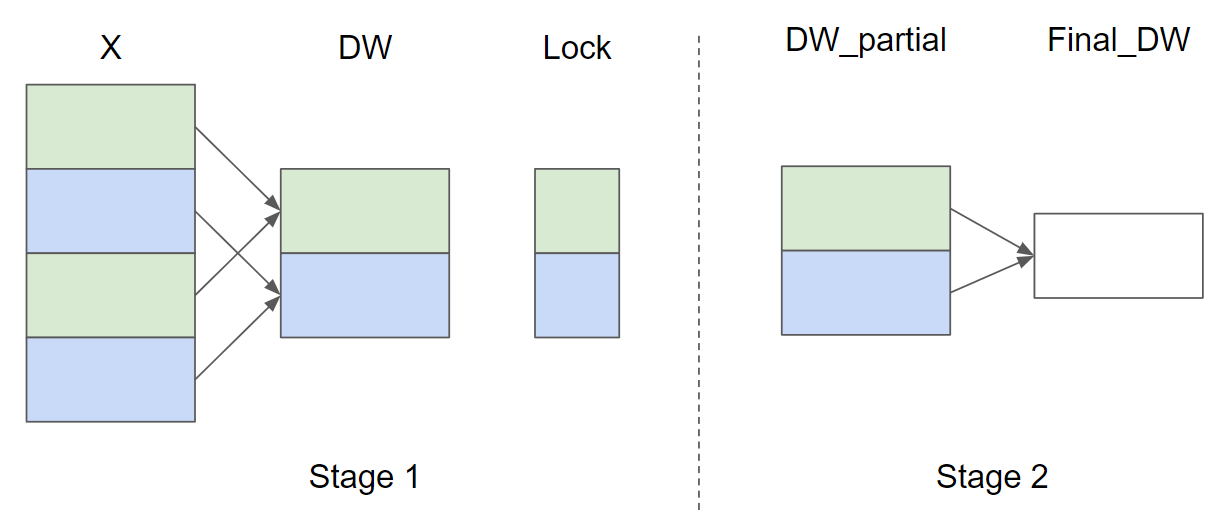
Since the same weights \(w\) and biases \(b\) are used for all rows in the same batch, their gradients need to sum up. To perform this step efficiently, we use a parallel reduction strategy: each kernel instance accumulates partial \(\nabla_{w}\) and \(\nabla_{b}\) across certain rows into one of \(\text{GROUP_SIZE_M}\) independent buffers. These buffers stay in the L2 cache and then are further reduced by another function to compute the actual \(\nabla_{w}\) and \(\nabla_{b}\).
Let the number of input rows \(M = 4\) and \(\text{GROUP_SIZE_M} = 2\), here’s a diagram of the parallel reduction strategy for \(\nabla_{w}\) (\(\nabla_{b}\) is omitted for brevity):
In Stage 1, the rows of X that have the same color share the same buffer and thus a lock is used to ensure that only one kernel instance writes to the buffer at a time.
In Stage 2, the buffers are further reduced to compute the final \(\nabla_{w}\) and \(\nabla_{b}\).
In the following implementation, Stage 1 is implemented by the function _layer_norm_bwd_dx_fused and Stage 2 is implemented by the function _layer_norm_bwd_dwdb.
@triton.jit
def _layer_norm_bwd_dx_fused(DX, # pointer to the input gradient
DY, # pointer to the output gradient
DW, # pointer to the partial sum of weights gradient
DB, # pointer to the partial sum of biases gradient
X, # pointer to the input
W, # pointer to the weights
B, # pointer to the biases
Mean, # pointer to the mean
Rstd, # pointer to the 1/std
Lock, # pointer to the lock
stride, # how much to increase the pointer when moving by 1 row
N, # number of columns in X
eps, # epsilon to avoid division by zero
GROUP_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr):
# Map the program id to the elements of X, DX, and DY it should compute.
row = tl.program_id(0)
cols = tl.arange(0, BLOCK_SIZE_N)
mask = cols < N
X += row * stride
DY += row * stride
DX += row * stride
# Offset locks and weights/biases gradient pointer for parallel reduction
lock_id = row % GROUP_SIZE_M
Lock += lock_id
Count = Lock + GROUP_SIZE_M
DW = DW + lock_id * N + cols
DB = DB + lock_id * N + cols
# Load data to SRAM
x = tl.load(X + cols, mask=mask, other=0).to(tl.float32)
dy = tl.load(DY + cols, mask=mask, other=0).to(tl.float32)
w = tl.load(W + cols, mask=mask).to(tl.float32)
mean = tl.load(Mean + row)
rstd = tl.load(Rstd + row)
# Compute dx
xhat = (x - mean) * rstd
wdy = w * dy
xhat = tl.where(mask, xhat, 0.)
wdy = tl.where(mask, wdy, 0.)
c1 = tl.sum(xhat * wdy, axis=0) / N
c2 = tl.sum(wdy, axis=0) / N
dx = (wdy - (xhat * c1 + c2)) * rstd
# Write dx
tl.store(DX + cols, dx, mask=mask)
# Accumulate partial sums for dw/db
partial_dw = (dy * xhat).to(w.dtype)
partial_db = (dy).to(w.dtype)
while tl.atomic_cas(Lock, 0, 1) == 1:
pass
count = tl.load(Count)
# First store doesn't accumulate
if count == 0:
tl.atomic_xchg(Count, 1)
else:
partial_dw += tl.load(DW, mask=mask)
partial_db += tl.load(DB, mask=mask)
tl.store(DW, partial_dw, mask=mask)
tl.store(DB, partial_db, mask=mask)
# Release the lock
tl.atomic_xchg(Lock, 0)
@triton.jit
def _layer_norm_bwd_dwdb(DW, # pointer to the partial sum of weights gradient
DB, # pointer to the partial sum of biases gradient
FINAL_DW, # pointer to the weights gradient
FINAL_DB, # pointer to the biases gradient
M, # GROUP_SIZE_M
N, # number of columns
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr):
# Map the program id to the elements of DW and DB it should compute.
pid = tl.program_id(0)
cols = pid * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
dw = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
db = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
# Iterate through the rows of DW and DB to sum the partial sums.
for i in range(0, M, BLOCK_SIZE_M):
rows = i + tl.arange(0, BLOCK_SIZE_M)
mask = (rows[:, None] < M) & (cols[None, :] < N)
offs = rows[:, None] * N + cols[None, :]
dw += tl.load(DW + offs, mask=mask, other=0.)
db += tl.load(DB + offs, mask=mask, other=0.)
# Write the final sum to the output.
sum_dw = tl.sum(dw, axis=0)
sum_db = tl.sum(db, axis=0)
tl.store(FINAL_DW + cols, sum_dw, mask=cols < N)
tl.store(FINAL_DB + cols, sum_db, mask=cols < N)
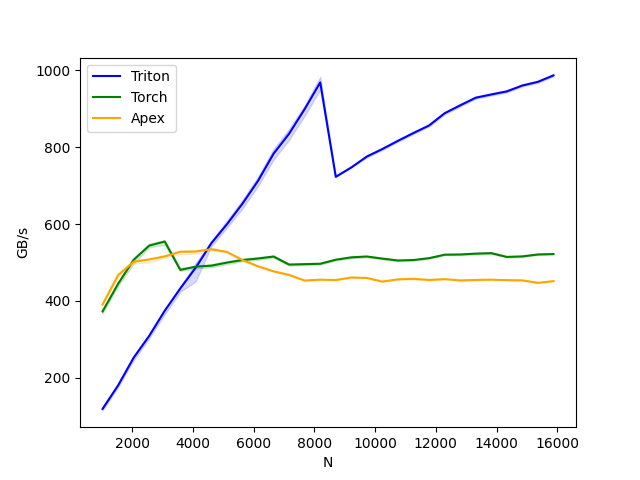
Benchmark¶
We can now compare the performance of our kernel against that of PyTorch.
Here we focus on inputs that have Less than 64KB per feature.
Specifically, one can set 'mode': 'backward' to benchmark the backward pass.
class LayerNorm(torch.autograd.Function):
@staticmethod
def forward(ctx, x, normalized_shape, weight, bias, eps):
# allocate output
y = torch.empty_like(x)
# reshape input data into 2D tensor
x_arg = x.reshape(-1, x.shape[-1])
M, N = x_arg.shape
mean = torch.empty((M, ), dtype=torch.float32, device='cuda')
rstd = torch.empty((M, ), dtype=torch.float32, device='cuda')
# Less than 64KB per feature: enqueue fused kernel
MAX_FUSED_SIZE = 65536 // x.element_size()
BLOCK_SIZE = min(MAX_FUSED_SIZE, triton.next_power_of_2(N))
if N > BLOCK_SIZE:
raise RuntimeError("This layer norm doesn't support feature dim >= 64KB.")
# heuristics for number of warps
num_warps = min(max(BLOCK_SIZE // 256, 1), 8)
# enqueue kernel
_layer_norm_fwd_fused[(M, )]( #
x_arg, y, weight, bias, mean, rstd, #
x_arg.stride(0), N, eps, #
BLOCK_SIZE=BLOCK_SIZE, num_warps=num_warps, num_ctas=1)
ctx.save_for_backward(x, weight, bias, mean, rstd)
ctx.BLOCK_SIZE = BLOCK_SIZE
ctx.num_warps = num_warps
ctx.eps = eps
return y
@staticmethod
def backward(ctx, dy):
x, w, b, m, v = ctx.saved_tensors
# heuristics for amount of parallel reduction stream for DW/DB
N = w.shape[0]
GROUP_SIZE_M = 64
if N <= 8192: GROUP_SIZE_M = 96
if N <= 4096: GROUP_SIZE_M = 128
if N <= 1024: GROUP_SIZE_M = 256
# allocate output
locks = torch.zeros(2 * GROUP_SIZE_M, dtype=torch.int32, device='cuda')
_dw = torch.empty((GROUP_SIZE_M, w.shape[0]), dtype=x.dtype, device=w.device)
_db = torch.empty((GROUP_SIZE_M, w.shape[0]), dtype=x.dtype, device=w.device)
dw = torch.empty((w.shape[0], ), dtype=w.dtype, device=w.device)
db = torch.empty((w.shape[0], ), dtype=w.dtype, device=w.device)
dx = torch.empty_like(dy)
# enqueue kernel using forward pass heuristics
# also compute partial sums for DW and DB
x_arg = x.reshape(-1, x.shape[-1])
M, N = x_arg.shape
_layer_norm_bwd_dx_fused[(M, )]( #
dx, dy, _dw, _db, x, w, b, m, v, locks, #
x_arg.stride(0), N, ctx.eps, #
BLOCK_SIZE_N=ctx.BLOCK_SIZE, #
GROUP_SIZE_M=GROUP_SIZE_M, #
num_warps=ctx.num_warps)
grid = lambda meta: [triton.cdiv(N, meta['BLOCK_SIZE_N'])]
# accumulate partial sums in separate kernel
_layer_norm_bwd_dwdb[grid](
_dw, _db, dw, db, GROUP_SIZE_M, N, #
BLOCK_SIZE_M=32, #
BLOCK_SIZE_N=128, num_ctas=1)
return dx, None, dw, db, None
layer_norm = LayerNorm.apply
def test_layer_norm(M, N, dtype, eps=1e-5, device='cuda'):
# create data
x_shape = (M, N)
w_shape = (x_shape[-1], )
weight = torch.rand(w_shape, dtype=dtype, device='cuda', requires_grad=True)
bias = torch.rand(w_shape, dtype=dtype, device='cuda', requires_grad=True)
x = -2.3 + 0.5 * torch.randn(x_shape, dtype=dtype, device='cuda')
dy = .1 * torch.randn_like(x)
x.requires_grad_(True)
# forward pass
y_tri = layer_norm(x, w_shape, weight, bias, eps)
y_ref = torch.nn.functional.layer_norm(x, w_shape, weight, bias, eps).to(dtype)
# backward pass (triton)
y_tri.backward(dy, retain_graph=True)
dx_tri, dw_tri, db_tri = [_.grad.clone() for _ in [x, weight, bias]]
x.grad, weight.grad, bias.grad = None, None, None
# backward pass (torch)
y_ref.backward(dy, retain_graph=True)
dx_ref, dw_ref, db_ref = [_.grad.clone() for _ in [x, weight, bias]]
# compare
assert torch.allclose(y_tri, y_ref, atol=1e-2, rtol=0)
assert torch.allclose(dx_tri, dx_ref, atol=1e-2, rtol=0)
assert torch.allclose(db_tri, db_ref, atol=1e-2, rtol=0)
assert torch.allclose(dw_tri, dw_ref, atol=1e-2, rtol=0)
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['N'],
x_vals=[512 * i for i in range(2, 32)],
line_arg='provider',
line_vals=['triton', 'torch'] + (['apex'] if HAS_APEX else []),
line_names=['Triton', 'Torch'] + (['Apex'] if HAS_APEX else []),
styles=[('blue', '-'), ('green', '-'), ('orange', '-')],
ylabel='GB/s',
plot_name='layer-norm-backward',
args={'M': 4096, 'dtype': torch.float16, 'mode': 'backward'},
))
def bench_layer_norm(M, N, dtype, provider, mode='backward', eps=1e-5, device='cuda'):
# create data
x_shape = (M, N)
w_shape = (x_shape[-1], )
weight = torch.rand(w_shape, dtype=dtype, device='cuda', requires_grad=True)
bias = torch.rand(w_shape, dtype=dtype, device='cuda', requires_grad=True)
x = -2.3 + 0.5 * torch.randn(x_shape, dtype=dtype, device='cuda')
dy = .1 * torch.randn_like(x)
x.requires_grad_(True)
quantiles = [0.5, 0.2, 0.8]
# utility functions
if provider == 'triton':
def y_fwd():
return layer_norm(x, w_shape, weight, bias, eps) # noqa: F811, E704
if provider == 'torch':
def y_fwd():
return torch.nn.functional.layer_norm(x, w_shape, weight, bias, eps) # noqa: F811, E704
if provider == 'apex':
apex_layer_norm = apex.normalization.FusedLayerNorm(w_shape).to(x.device).to(x.dtype)
def y_fwd():
return apex_layer_norm(x) # noqa: F811, E704
# forward pass
if mode == 'forward':
gbps = lambda ms: 2 * x.numel() * x.element_size() / ms * 1e-6
ms, min_ms, max_ms = triton.testing.do_bench(y_fwd, quantiles=quantiles, rep=500)
# backward pass
if mode == 'backward':
def gbps(ms):
return 3 * x.numel() * x.element_size() / ms * 1e-6 # noqa: F811, E704
y = y_fwd()
ms, min_ms, max_ms = triton.testing.do_bench(lambda: y.backward(dy, retain_graph=True), quantiles=quantiles,
grad_to_none=[x], rep=500)
return gbps(ms), gbps(max_ms), gbps(min_ms)
test_layer_norm(1151, 8192, torch.float16)
bench_layer_norm.run(save_path='.', print_data=True)
layer-norm-backward:
N Triton Torch Apex
0 1024.0 118.724635 372.363633 390.095241
1 1536.0 179.824387 444.144584 466.632925
2 2048.0 252.061538 506.721668 501.551037
3 2560.0 308.743716 543.716805 507.768606
4 3072.0 374.253805 554.345889 515.580429
5 3584.0 432.241202 480.536326 527.705508
6 4096.0 486.653476 489.074621 528.516116
7 4608.0 550.208948 491.520008 534.260858
8 5120.0 599.414623 499.512174 527.381977
9 5632.0 652.985493 506.247199 506.247199
10 6144.0 712.347810 510.228394 489.887055
11 6656.0 783.058838 515.303221 476.847776
12 7168.0 835.106808 494.344826 467.478250
13 7680.0 899.121934 495.483858 452.874677
14 8192.0 968.512300 496.484863 455.111110
15 8704.0 722.823558 507.029134 454.121729
16 9216.0 747.243211 513.187943 460.800012
17 9728.0 775.654504 515.390744 459.590527
18 10240.0 795.339817 509.875515 450.109870
19 10752.0 816.607619 504.986310 455.915192
20 11264.0 836.953598 506.247199 457.421306
21 11776.0 856.436338 511.074123 454.379406
22 12288.0 888.289167 520.126975 456.520144
23 12800.0 908.875706 520.677957 453.097357
24 13312.0 928.744186 522.893621 454.463728
25 13824.0 937.220368 524.132711 455.111098
26 14336.0 945.230752 514.295986 453.910285
27 14848.0 960.517515 515.704759 453.374052
28 15360.0 970.105232 520.677982 446.836366
29 15872.0 986.860104 521.819157 451.336480
References¶
Jimmy Lei Ba and Jamie Ryan Kiros and Geoffrey E. Hinton, “Layer Normalization”, Arxiv 2016
Total running time of the script: (0 minutes 44.028 seconds)